Much has changed since the early days of MRI, when the pioneers of the field – among them, Raymond Damadian, Paul Lauterbur, and Peter Mansfield – first grappled with the inherent speed bottleneck of MR imaging. Modern MRI has benefited from the accumulation of technological advances and ingenious imaging strategies developed over the past 4 decades. MRI researchers continue to push for faster image acquisitions, attempting to strike a tricky balance between improving scan time efficiency and preserving image quality.
I’ve spent much of the past few months learning about different imaging strategies that aim to achieve this elusive goal. Through this blog series, I will provide an overview of image acquisition and reconstruction methods used in structural MRI, ranging from canonical to cutting-edge approaches. This is inspired in part by a recent review article, which offers a bird’s-eye view of existing optimization frameworks for image reconstruction. In the first installment of this series, I introduce fundamental concepts in MR signal acquisition and motivate the need for accelerated imaging.
MR Signal Acquisition
During an MRI scan, the signals we acquire correspond to the spatial frequency components (referred to as \(k\)-space ) of the image we want to obtain. This is mathematically represented by the MR signal equation, which relates our acquired signal \(s(\vec{k})\) and the desired image \(m(\vec{r})\): \[s(\vec{k}) = \int_V {m(\vec{r}) e^{-i2 \pi \vec{k} \dot{} \vec{r}} d\vec{r}} .\] This equation describes a Fourier Transform (FT) that maps between the image domain (\(\vec{r}\)) and k-space (\(\vec{k}\)).
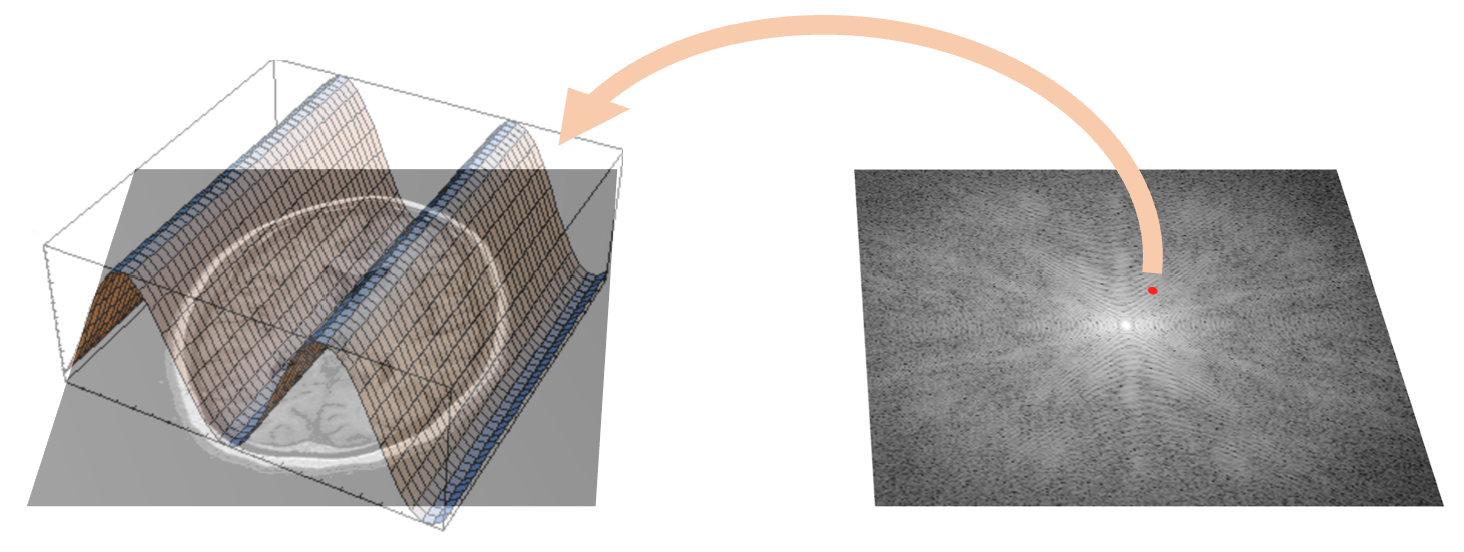
Within \(k\)-space, the low spatial frequencies capture the smooth underlying structures observed in the image, giving rise to its overall contours. In contrast, high spatial frequencies account for the fine details of the image, such as edges and intricate textures. Given a "well-sampled" \(k\)-space that falls on a regular Cartesian grid, we can simply retrieve our image by applying the inverse Fourier transform (IFT) to our acquired k-space data. But what constitutes a "well-sampled" \(k\)-space?

Sampling k-space
Acquiring an MR image involves making discrete, digitized samples of k-space. As a property of the FT, the resolution of the MR image, say, along the \(x\)-dimension (\(\delta{x}\)) will be inversely proportional to the chosen sampling step-size along the \(k_x\) dimension (\(\delta{k_x}\)). In particular, \( \delta{k_x} = {1 \over {N_x * \delta{x}}}\) where \( N_x \) is the number of pixels along the \( x \)-dimension of the image; multiplying \( N_x * \delta{x}\) gives us the field-of-view along this dimension (\( FOV_x\)). As such, the choice of \(k\)-space sampling step-size determines the \(FOV\) of the resulting image.
Here we come to the Shannon-Nyquist Sampling Theorem , which governs what it means to have a "well-sampled" \(k\)-space. In general, this theorem states that an analog signal needs to be sampled at a rate at least twice as large as the highest frequency contained in the signal. If we fall short of this criterion, the digitized signal will be \( \it{aliased}\) - it no longer accurately represents the original signal.
In the context of MRI, this theorem places an upper bound on the value of \( \delta{k}\) that would allow for proper image reconstruction. If we choose an insufficiently small \( \delta{k}\) and attempt to reconstruct our image, the signal aliasing that arises from violating the Shannon-Nyquist Sampling Theorem will manifest as image artifacts.
Towards Accelerated Imaging
Due to the Shannon-Nyquist Sampling Theorem, there is a minimum \(k\)-space sampling density to be met if we wish to carry out the standard FT-based image reconstruction. How quickly an image can be acquired is then determined by the hardware limitations of the MRI scanner. Considering an image with a reasonable matrix size of \( 256 \times 256 \times 192 \) pixels, this amounts to over \(12.6\) million \(k\)-space samples. Rather than resigning to abide by the speed limits set by MRI hardware, several approaches to overcome the Shannon-Nyquist Sampling criterion have been proposed over the years. In the next installment of this series, I will cover two of the most influential approaches: parallel imaging and compressed sensing.